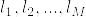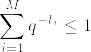情報通信システム 其の二 20170420

平均符号長とは

　

で表すことができる。

瞬時複合：境界で瞬時にどの符号を表しているのかがわかる複合

一意複合よりも瞬時複合のほうが嬉しい

そもそも2章でやっていくのは下の写真のところ

一意複合の下に瞬時複合がある理由はこの後説明していく

符号についてもう少し用語を…。

　・記憶がある：生起確率が独立

　・記憶がない：ほかの確率の生起に生起確率が影響を受けてしまう

　・定常情報源：生起確率が他の要因によって変化しない

符号化の性質

　・符号の木：二分木のようなもの。大本をroot、節をnode、branch、末端のleafで猛省される木構造。これを用いると瞬時複合可能かどうかが一発でわかる。

　・語頭条件

　　　瞬時複合可能であることの必要十分条件はどの符号語もほかの符号語の親にならないことに等しい

　　　つまり、すべての符号語がleafに存在していればその符号化は瞬時複合可能なものであるということ

　・クラフトの不等式

　　　長さの元符号が瞬時符号を持つための条件は

　　　　　

　　　である。この条件を満たしていても必ず瞬時複合可能かはわからない。あくまでそのような組み合わせが存在しうるといっているだけ。

　・マクミランの不等式

　　　ある符号化について

　　　　

　　　が成り立つとき、その符号化は一意複合可能である。これは逆側も成り立つ。クラフトの不等式と条件はおなじ。

 　　　　⇒したがって、一意複合可能である符号化は瞬時複合が可能な場合がある。

ハフマン符号化法

　コンパクト符号を生成するための符号化

　　→コンパクト符号：情報源を符号化したもののなかで、平均符号長が最小になるもの

　方法(元符号化をする場合に一般化する)

　　①生起確率が小さいものから順に個ずつつなげていく

　　②分岐を個の数で分岐させる

　　③根のほうからたどっていき、符号を決定していく

　⇒この方法をとると生起確率が小さいデータに長い符号があてられるのでコンパクト符号に自動的になる。

　実行例：ここでは、=2としてハフマン符号化を行っている

　一つに決まるとは限らないが、平均符号長はいずれの場合も同じになり、最小である。

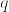　によって帳尻が合わないこともあるが、その場合はダミーを用いたりしてつじつまを合わせる。

　下に演習問題の解答例を載せておきます。