インタラクティブシステム論 其の二 20170420
フーリエ変換
人間自体、体の中(内耳の蝸牛管)でフーリエ変換をしている
⇒音は耳の奥の時点で空間情報に変換されている(周波数分解されている)
⇒ちなみに触覚も、皮膚に触れた瞬間に別次元の情報に変化されて脳に送られている
物理現象の多くは線形な微分方程式で書くことができる
⇒入力が正弦波ならば出力も同じ周期の正弦波になる(位相、振幅は変化する)
⇒波の中に含まれる正弦波の成分を調べたい
波fに波gはどれだけ含まれるか
⇒内積をとればいい
離散の場合
連続の場合
で波gの成分を求めることができる
したがって周期T、各周波数nω(第n高調波)のsin波は
だけ含まれていて、cos波は
だけ含まれていることがわかる
このaとbを用いることで波fは次のように変換することができる
n=0の時は計算できるのでちょっと簡略化
これがフーリエ級数展開
しかし、これだけでは
①分解法が一意か
②結果を合成して元に戻るか
がわからない。また、こうなるのは極めて希少なパターン。
⇒成分同士が直交していれば①②の性質は保証される
したがって
がnとmが違う値の時0になればいい。
証明は写真で(cosとcosの直交性のみ)。

複素フーリエ級数展開
であることを用いてフーリエ級数展開を書き直していく
と置くと
と導出することができる
これを複素フーリエ級数展開という。もちろんこれも任意のnについて直交性が保証されている。
フォルマント
人は母音や子音を認識する際、アクセントの強さを聞き取り認識している。その時、一番初めにアクセントが来るところを第一フォルマント、二番目を第二フォルマントという。この仕組みを応用させると「しゃべるピアノ」のようなものも作ることができる。
課題
矩形波、三角波、正弦波のスペクトルの違いをSciLabを用いて観察し、実際その違いが音色にどのような影響をもたらしているのかを考察して提出する。
g(i).png)
g(t)dt.png)
%5Csin(2%5Cpi%20t/T)dt.png)
%5Ccos(2%5Cpi%20t/T)dt.png)
%3D%5Csum_%7Bn%3D0%7D%5E%7B%5Cinfty%7D(a_n%5Ccos(2%5Cpi%20nt/T)+b_n%5Csin(2%5Cpi%20nt/T)).png)
%3Da_0+%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D(a_n%5Ccos(2%5Cpi%20nt/T)+b_n%5Csin(2%5Cpi%20nt/T)).png)
%5Ccos(2%5Cpi%20mt/T)dt.png)
%5Csin(2%5Cpi%20mt/T)dt.png)
%5Csin(2%5Cpi%20mt/T)dt.png)
.png)
.png)
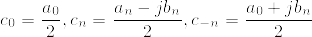
%3Dc_0+%5Csum_%7Bn%3D1%7D%5E%7BN%7D(c_ne%5E%7Bjn%5Comega%20t%7D+c_%7B-n%7De%5E%7B-jn%5Comega%20t%7D)%3D%5Csum_%7Bn%3D-%5Cinfty%7D%5E%7B%5Cinfty%7Dc_ne%5E%7Bjn%5Comega%20t%7D.png)